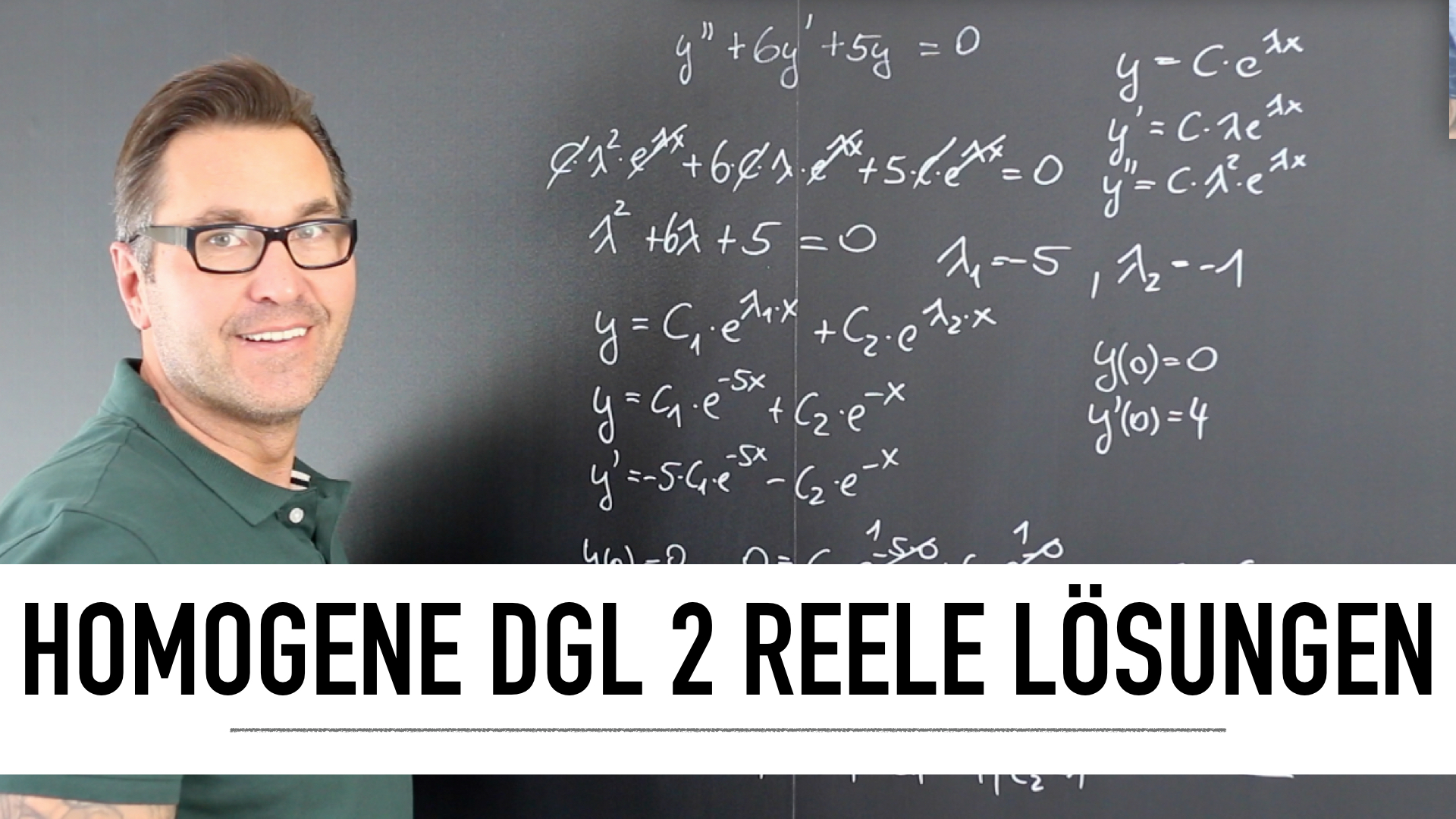Die mehrdimensionale Analysis betrachtet Funktionen mehrerer reeller Variablen, die oft als ein Vektor beziehungsweise n-Tupel dargestellt werden. Wir kennen bisher Differential- und Integralrechnung für Funktionen, die von einer Variablen abhängen. In Informatikgebieten wie Optimierung und Visual Computing spielen jedoch sehr oft Funktionen eine Rolle, die von mehreren Variablen abhängen. Die Ableitungsregeln für Funktionen einer Variabler übertragen sich direkt auf Funktionen mehrerer Variablen.

Viele Lehrbücher unterscheiden zwischen Analysis in einer und Analysis in mehreren Dimensionen. Diese Differenzierung berührt die grundlegenden Konzepte nicht, allerdings gibt es in mehreren Dimensionen eine größere mathematische Vielfalt. Die Begriffe der Norm (als Verallgemeinerung des Betrags), der Konvergenz, der Stetigkeit und der Grenzwerte lassen sich einfach von einer in mehrere Dimensionen verallgemeinern.

Wie ist die mehrdimensionale Analysis zu verstehen?

Die Differentiation von Funktionen mehrerer Variablen unterscheidet sich von der →eindimensionalen Differentiation. Wichtige Konzepte sind die Richtungs- und die partielle Ableitung, die Ableitungen in einer Richtung beziehungsweise in einer Variable sind. Der Satz von Schwarz stellt fest, wann partielle beziehungsweise Richtungsableitungen unterschiedlicher Richtungen vertauscht werden dürfen. Außerdem ist der Begriff der totalen Differentiation von Bedeutung. Diesen kannst du als die lokale Anpassung einer linearen Abbildung an den Verlauf der mehrdimensionalen Funktion interpretieren und als das mehrdimensionale Analogon der (eindimensionalen) Ableitung verstehen. 

Der Satz von der impliziten Funktion über die lokale, eindeutige Auflösung impliziter Gleichungen ist eine wichtige Aussage der mehrdimensionalen Analysis und kann als eine Grundlage der Differentialgeometrie verstanden werden.

In der mehrdimensionalen Analysis gibt es unterschiedliche Integralbegriffe wie das Kurvenintegral, das Oberflächenintegral und das Raumintegral. Jedoch von einem abstrakteren Standpunkt aus der Vektoranalysis unterscheiden sich diese Begriffe nicht. Zum Lösen dieser Integrale sind der Transformationssatz als Verallgemeinerung der Substitutionsregel und der Satz von Fubini, welcher es erlaubt, Integrale über n-dimensionale Mengen in iterierte Integrale umzuwandeln, von besonderer Bedeutung. 

Auch die Integralsätze aus der Vektoranalysis von Gauß, Green und Stokes sind in der mehrdimensionalen Analysis von Bedeutung. Du kannst sie als Verallgemeinerung des Hauptsatzes der Integral- und Differentialrechnung verstehen.

Für quadratische Matrizen gibt es bestimmte Vektoren, die man an die Matrix multiplizieren kann. Sodass man den selben Vektor als Ergebnis erhält, nur mit einem Vorfaktor multipliziert. Solch einen Vektor nennt man Eigenvektor und der Vorfaktor heißt →Eigenwert einer Matrix.

Anhand der Eigenwerte kann man die Definitheit einer Matrix bestimmen. So sind die Eigenwerte von reellen symmetrischen Matrizen reell. Ist die Matrix echt positiv definit so sind die Eigenwerte reell und echt größer Null.

Eigenvektoren einer Abbildung sind in der linearen Algebra vom Nullvektor verschiedene Vektoren, dessen Richtung durch die Abbildung nicht verändert wird. Eigenvektoren skaliert man und bezeichnet den Skalierungsfaktor als →Eigenwert der Abbildung.

Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssystem eindeutig lösbar ist oder nicht. 

In vielen Anwendungen beschreiben Eigenwerte auch physikalische Eigenschaften eines mathematischen Modells. Die Verwendung der Vorsilbe „Eigen-“ für charakteristische Größen in diesem Sinne lässt sich auf eine Veröffentlichung von David Hilbert aus dem Jahre 1904 zurückführen.

Eigenvektor und Eigenwerte haben folgende Eigenschaften

Die Eigenvektoren sind nur bis auf einen Faktor bestimmt. Wenn x ein Eigenvektor ist, dann gilt das auch für q⋅x  mit beliebigem q.

Ist λ ein Eigenwert der →invertierbaren Matrix A zum Eigenvektor x, so ist 1/λ Eigenwert der inversen Matrix von A zum Eigenvektor x.

Alle Eigenwerte sind stets reell. Im Rahmen der Hauptachsentransformation nennt man die Eigenwerte auch Hauptwerte. Ist die Matrix zudem positiv definit, so sind auch ihre Eigenwerte echt positiv.

Es lässt sich immer eine Orthonormalbasis aus Eigenvektoren angeben.Dies ist eine direkte Folgerung aus dem Spektralsatz. Insbesondere sind Eigenvektoren zu verschiedenen Eigenwerten zueinander orthogonal.

Ein Eigenwert hat unendlich viele zugehörige Eigenvektoren, während ein Eigenvektor immer nur zu einem Eigenwert gehören kann. Multipliziert man die Matrix A mit dem k -fachen Eigenvektor, bleibt der dazu gehörende Eigenwert λ unverändert.

Eigenvektoren sind eindeutig bestimmt, bis auf die Multiplikation mit einem Skalar. Das heißt: Wenn x ein Eigenvektor und a ein Skalar ist, dann ist auch a * x ein Eigenvektor

Differentialgleichungen lassen sich in homogene und inhomogene Differentialgleichungen unterscheiden. Die Lösung einer inhomogenen DGL besteht aus der allgemeinen Lösung der homogenen und einer speziellen Lösung (partikuläre Lösung) der inhomogenen DGL. Deshalb erfolgt das Lösungsverfahren der inhomogenen DGL, unabhängig von der Ordnung, in zwei Stufen. Dabei ist die Gesamtlösung die Summe der beiden Lösungen.

Die homogene Lösung der DGL ist Null, wenn alle Anfangsbedingungen und deren Ableitungen Null sind. Die partikuläre Lösung der DGL beschreibt das Übertragungsverhalten als erzwungene Bewegung. Je nach Systemordnung müssen alle Anfangsbedingungen y und deren Ableitungen Null sein. Die partikuläre Lösung der DGL ist in der Regelungstechnik meist von hauptsächlichem Interesse.

Mit Hilfe des Exponentialansatzes und der sich daraus ergebenden charakteristischen Gleichung lassen sich auch DGL höherer Ordnung lösen. Dieser Exponentialansatz gilt als universelles Lösungsverfahren für homogene DGL beliebiger Ordnungen mit konstanten Koeffizienten.

Wie löse ich inhomogene Differentialgleichungen?

Die Variation der Konstanten ist ein Verfahren aus der Theorie linearer gewöhnlicher Differentialgleichungen. Diese nutzt man zur Bestimmung einer speziellen Lösung eines inhomogenen linearen Differentialgleichungssystems erster Ordnung. Und einer inhomogenen linearen Differentialgleichung beliebiger Ordnung. Vorausgesetzt wird hierfür eine vollständige Lösung (Fundamentalsystem) der zugehörigen homogenen Differentialgleichung.

Wenn du eine inhomogene Differentialgleichung vor dir hast, bestimmst du die Lösung in zwei Schritten: Du berechnest die homogene Lösung  und die sogenannte partikuläre Lösung, auch spezielle Lösung der inhomogenen Gleichung genannt. Zusammen ergeben sie die Gesamtlösung.

Eine inhomogene lineare Differentialgleichung 1. Ordnung lässt sich durch Variation der Konstanten auf folgende Weise lösen. Zuerst löst du die entsprechende homogene Differentialgleichung durch Trennung der Variablen. Um die inhomogene DGL zu lösen, ersetzt du die Integrationskonstante C durch eine unbekannte Funktion C (x). Die Funktionsterme für y und y‘ setzt du in die inhomogene DGL ein. Diesen Ausdruck für C (x) setzt du in die Formel für y ein und erhälst die allgemeine Lösung der inhomogenen DGL. Diese Methode ist als Methode der Variation der Konstanten bekannt. Die Integrationskonstante C wird variiert, das heißt durch eine Funktion C(x) ersetzt.

Das Lösen einer Differentialgleichung höherer Ordnung ist äquivalent zum Lösen eines geeigneten Differentialgleichungssystems erster Ordnung. Auf diese Weise kann man obiges Verfahren nutzen, um eine spezielle Lösung für eine Differentialgleichung höherer Ordnung zu konstruieren.