Der Box-Plot (auch Box-Whisker-Plot, Kastenschaubild oder Kastengrafik) ist ein Diagramm, das zur grafischen Darstellung der Verteilung eines mindestens ordinalskalierten Merkmals verwendet wird. Es fasst dabei verschiedene robuste Streuungs- und Lagemaße in einer Darstellung zusammen. Ein Box-Plot kann dir sehr schnell einen Eindruck darüber vermitteln, in welchem Bereich die Daten liegen und wie sie sich über diesen Bereich verteilen. Deshalb werden alle Werte der sogenannten Fünf-Punkte-Zusammenfassung, also der Median, die zwei Quartile und die beiden Extremwerte, dargestellt.

Ein Box-Plot besteht immer aus einem Rechteck, genannt Box, und zwei Linien, die dieses Rechteck verlängern. Diese Linien werden als „Antenne“ oder seltener als „Fühler“ oder „Whisker“ bezeichnet und werden durch einen Strich abgeschlossen. Das Ende der Antennen beschreibt in weiterer Folge das Minimum und das Maximum. In der Regel repräsentiert der Strich in der Box den Median (Q2) der Verteilung. Das Ende der Box beschreibt links das Q1 und rechts das Q3

Was ist ein Box Plot?

Die Box entspricht dem Bereich, in dem die mittleren 50 % der Daten liegen. Sie wird also durch das obere und das untere Quartil (Q1 & Q3) begrenzt, und die Länge der Box entspricht dem sogenannten Interquartilsabstand. Dieser ist ein Maß der Streuung der Daten und wird durch die Differenz des oberen und unteren Quartils bestimmt (Q3 – Q1). Des Weiteren wird der Median als durchgehender Strich in der Box eingezeichnet. Dieser Strich teilt das gesamte Diagramm in zwei Bereiche, in denen jeweils 50 % der Daten liegen. Durch seine Lage innerhalb der Box bekommst du also einen Eindruck von der Verteilung der Daten vermittelt. Ist der Median im linken Teil der Box, so ist die Verteilung rechtsschief, ist er im rechten Teil der Box kannst du von einem linksschiefen Boxplot sprechen.

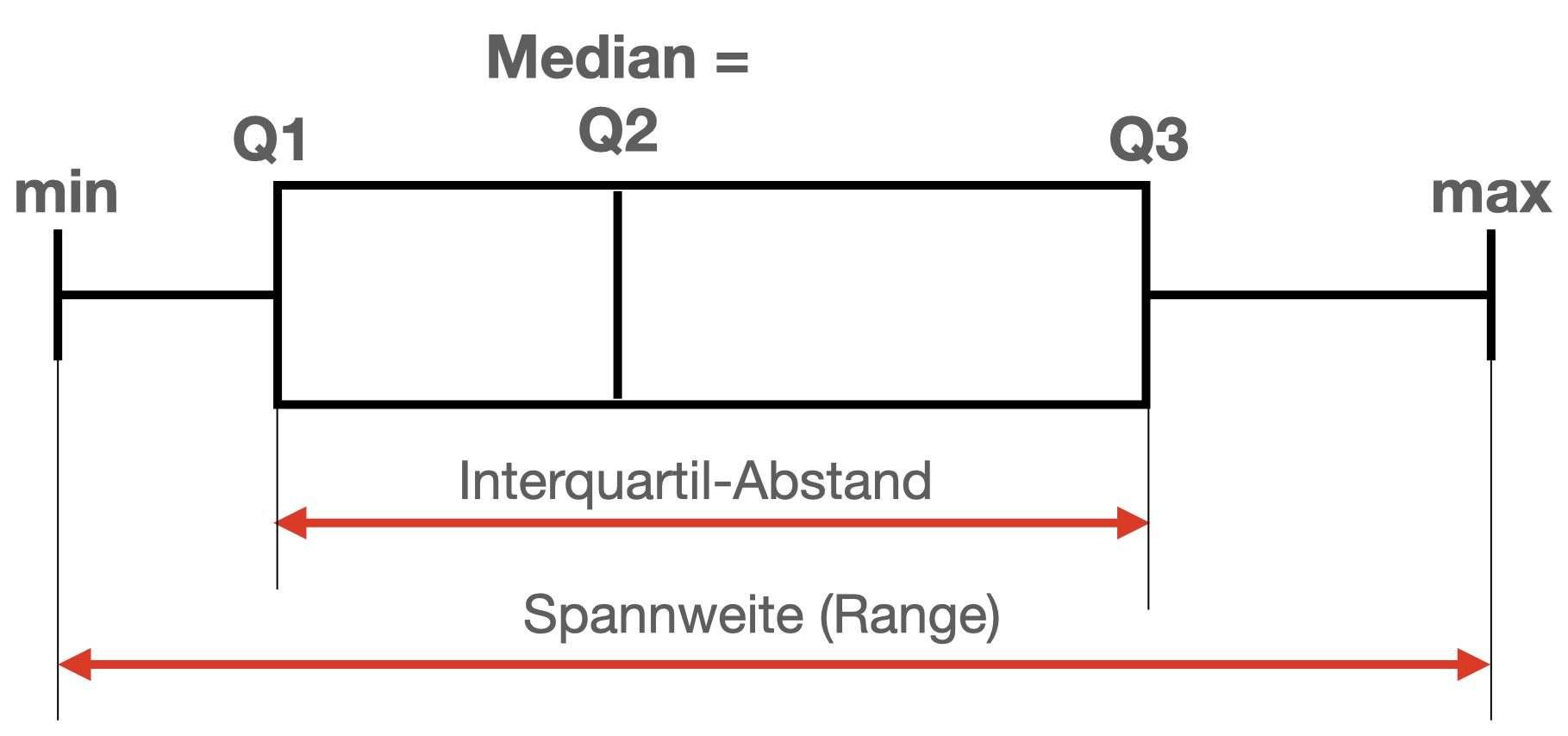Aufgrund des einfachen Aufbaus von Box-Plots verwendest du diese immer dann, wenn du dir schnell einen Überblick über bestehende Daten verschaffen willst. Dabei muss nicht bekannt sein, welcher Verteilung diese Daten unterliegen. Die Box gibt an, in welchem Bereich 50 % der Daten liegen. An der Lage des Medians innerhalb dieser Box kannst du erkennen, ob eine Verteilung symmetrisch oder schief ist. 

Box-Plots eignen sich auch, um eventuelle Ausreißer zu identifizieren, oder liefern Hinweise darauf, ob die Daten einer bestimmten Verteilung unterliegen. 

Wenn der Box-Plot stark asymmetrisch ist, eine ungewöhnlich hohe Ausreißerzahl oder weit von der Box entfernte Ausreißer enthält, deutet das beispielsweise darauf hin, dass die Daten nicht normalverteilt sind.

Der wesentliche Vorteil des Box-Plot besteht im raschen Vergleich der Verteilung in verschiedenen Untergruppen. Während ein Histogramm eine zweidimensionale Ausdehnung hat, ist ein Box-Plot im Wesentlichen eindimensional. So lassen sich leicht mehrere Datensätze nebeneinander (oder untereinander bei waagerechter Darstellung) auf derselben Skala darstellen und vergleichen.