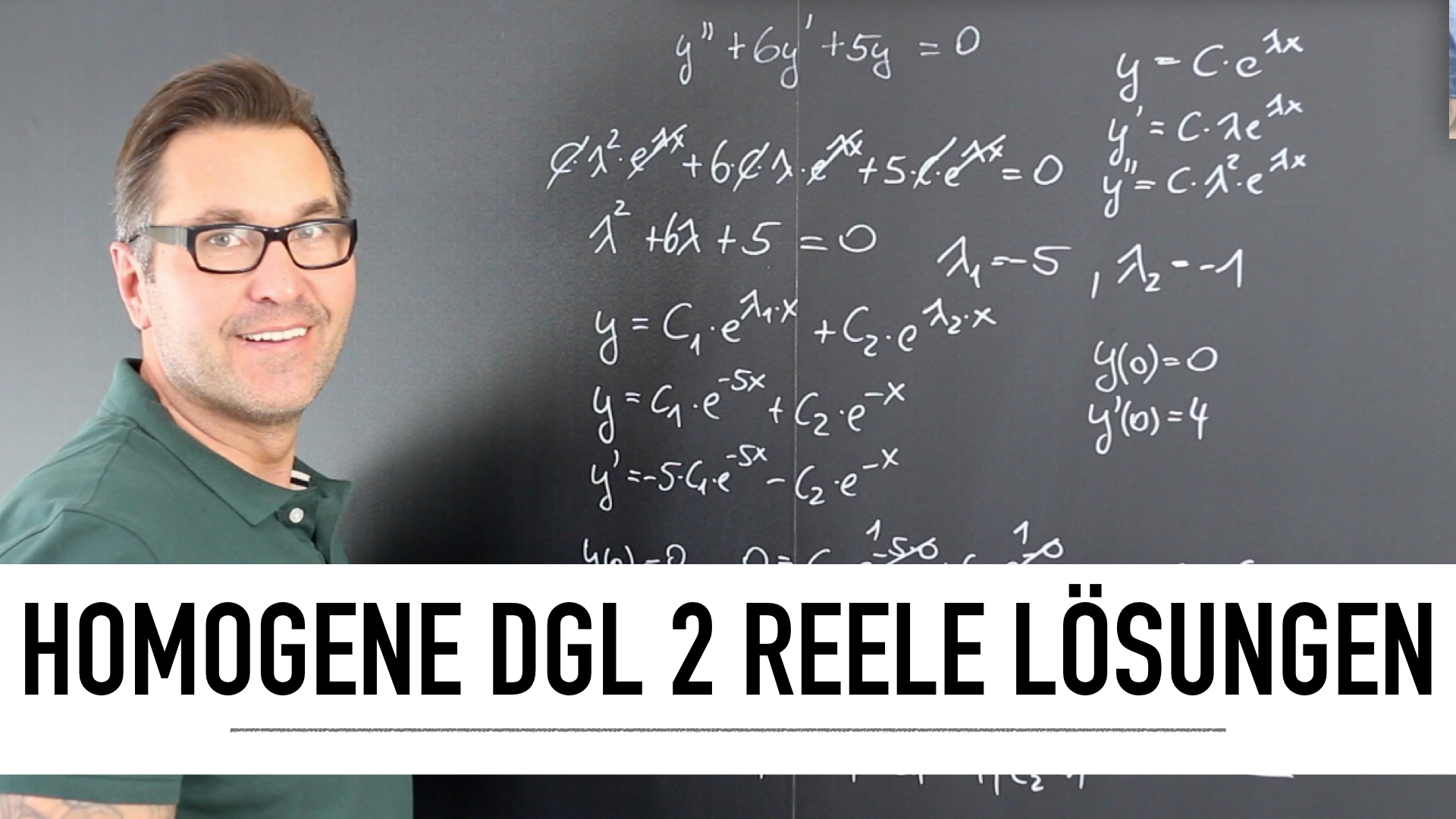
Differentialgleichungen lassen sich in homogene und inhomogene Differentialgleichungen unterscheiden. Die Lösung einer inhomogenen DGL besteht aus der allgemeinen Lösung der homogenen und einer speziellen Lösung (partikuläre Lösung) der inhomogenen DGL. Deshalb erfolgt das Lösungsverfahren der inhomogenen DGL, unabhängig von der Ordnung, in zwei Stufen. Dabei ist die Gesamtlösung die Summe der beiden Lösungen.

Die homogene Lösung der DGL ist Null, wenn alle Anfangsbedingungen und deren Ableitungen Null sind. Die partikuläre Lösung der DGL beschreibt das Übertragungsverhalten als erzwungene Bewegung. Je nach Systemordnung müssen alle Anfangsbedingungen y und deren Ableitungen Null sein. Die partikuläre Lösung der DGL ist in der Regelungstechnik meist von hauptsächlichem Interesse.

Mit Hilfe des Exponentialansatzes und der sich daraus ergebenden charakteristischen Gleichung lassen sich auch DGL höherer Ordnung lösen. Dieser Exponentialansatz gilt als universelles Lösungsverfahren für homogene DGL beliebiger Ordnungen mit konstanten Koeffizienten.

Wie löse ich inhomogene Differentialgleichungen?

Die Variation der Konstanten ist ein Verfahren aus der Theorie linearer gewöhnlicher Differentialgleichungen. Diese nutzt man zur Bestimmung einer speziellen Lösung eines inhomogenen linearen Differentialgleichungssystems erster Ordnung. Und einer inhomogenen linearen Differentialgleichung beliebiger Ordnung. Vorausgesetzt wird hierfür eine vollständige Lösung (Fundamentalsystem) der zugehörigen homogenen Differentialgleichung.

Wenn du eine inhomogene Differentialgleichung vor dir hast, bestimmst du die Lösung in zwei Schritten: Du berechnest die homogene Lösung  und die sogenannte partikuläre Lösung, auch spezielle Lösung der inhomogenen Gleichung genannt. Zusammen ergeben sie die Gesamtlösung.

Eine inhomogene lineare Differentialgleichung 1. Ordnung lässt sich durch Variation der Konstanten auf folgende Weise lösen. Zuerst löst du die entsprechende homogene Differentialgleichung durch Trennung der Variablen. Um die inhomogene DGL zu lösen, ersetzt du die Integrationskonstante C durch eine unbekannte Funktion C (x). Die Funktionsterme für y und y‘ setzt du in die inhomogene DGL ein. Diesen Ausdruck für C (x) setzt du in die Formel für y ein und erhälst die allgemeine Lösung der inhomogenen DGL. Diese Methode ist als Methode der Variation der Konstanten bekannt. Die Integrationskonstante C wird variiert, das heißt durch eine Funktion C(x) ersetzt.

Das Lösen einer Differentialgleichung höherer Ordnung ist äquivalent zum Lösen eines geeigneten Differentialgleichungssystems erster Ordnung. Auf diese Weise kann man obiges Verfahren nutzen, um eine spezielle Lösung für eine Differentialgleichung höherer Ordnung zu konstruieren.

Zeichnet man eine beliebige Raumdiagonale des Quaders ein (z.B. jene vom Eckpunkt B zum Eckpunkt H), so entsteht ein rechtwinkeliges Dreieck (rechter Winkel im Eckpunkt D). In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Raumdiagonale berechnen.

Wie berechne ich die Raumdiagonale?

Die Diagonale r von einer zur gegenüberliegenden Ecke hat die Länge der Wurzel aus (a²+b²+c²), wie leicht durch zweimalige →Anwendung des Satzes des Pythagoras zu berechnen ist. Ein Quader ist durch drei Angaben stets eindeutig bestimmt. Dieser hat 8 Ecken, die gegen den Uhrzeigersinn in Großbuchstaben beschriftet werden und besteht aus 6 Begrenzungsflächen (Rechtecke), von denen jeweils 2 gleich groß sind. Gegenüberliegende Begrenzungsflächen eines Quaders sind kongruent (deckungsgleich).

Wie viele Grundflächen hat ein Würfel?

Der Würfel hat 8 Ecken, 12 Kanten und 6 Flächen. Jeweils vier Kanten des Quaders sind gleich lang.

Ein Würfel (auch Hexaeder/Sechsflächner/Kubus genannt) ist ein geometrischer Körper, der aus 6 aneinanderliegenden Quadratflächen besteht (Begrenzungsflächen). Alle Seiten der Quadratflächen haben die gleiche Länge und stehen senkrecht aufeinander, zwei Seiten liegen jeweils parallel gegenüber.

Für Würfel gelten folgende Formeln: Ist a die Kantenlänge, so ist das Volumen gleich a*a*a; die Oberfläche ist gleich 6*a*a und die Grundfläche hat den Flächeninhalt a*a. Die Diagonalen auf einer Seite haben jeweils die Länge Wurzel aus (a²+a²), da sie einfach Diagonalen eines Quadrates sind.

Jeder Würfel hat sechs Flächen, die aus gleich großen Quadraten bestehen. Daher besitzt ein Würfel acht Ecken und zwölf gleich lange Kanten. Die Kanten des Würfels bilden zueinander rechte Winkel. Ein Würfel ist also ein spezieller Quader, da alle Kanten gleich lang sind.

Da es sich bei den Seitenflächen um Quadrate handelt, sind die jeweiligen 4 Eckpunkte einer Seitenfläche gleich weit von Mittelpunkt dieser Fläche entfernt. Die Beschriftung der Eckpunkte erfolgt mit Großbuchstaben und gegen den Uhrzeigersinn.

Eine Sinusschwingung ist eine regelmäßige (periodische) Schwingung um einen Nullpunkt. Ihre Maßeinheit ist Schwingung pro Sekunde, gleich Hertz. Zur Beschreibung einer harmonischen Schwingung wird im Allgemeinen die →Sinusfunktion verwendet. In der Form:

𝑦(𝑡)=𝑦⋅sin(𝜔⋅𝑡 + ϕ)  oder 𝑦(𝑡)=𝑦⋅sin(2𝜋𝑇⋅𝑡 + ϕ)

Hierbei hat die Schwingung zur Zeit 𝑡=0 die Auslenkung (Elongation) null und beginnt in die positive 𝑦-Richtung zu schwingen.

• Bei einer periodischen Bewegung hat ein Körper nach einer Periodendauer 𝑇  wieder den gleichen Bewegungszustand
• Dabei gilt für die Frequenz einer periodischen Bewegung gilt 𝑓=1/𝑇
• Die Amplitude einer Schwingung ist der Betrag des Maximalwerts der Auslenkung aus der Ruhelage.

Eine Sinus Funktion erhalten wir, wenn wir mit einem Messgerät an unsere Steckdose gehen und die Spannung aufzeichnen. Der →Graph zeigt einen Sinus-Verlauf der Funktion y = sin(x).

Wie auch bei normalen Gleichungen, kann man für das x verschiedene Werte einsetzen. Wobei du in einfachen Beispielen am Besten die Werte 0, π/2, π, 3π/2 und 2π in die Gleichung einsetzt (Taschenrechner auf RAD stellen ). Je nach Mathelehrer und Bundesland können noch Begriffe wie Amplitude, Schwingdauer, Frequenz und Phase im Unterricht auftauchen.

Was ist die harmonische Sinusschwingung?

Die harmonische Schwingung ist somit definiert als die durch den Schatten eines gleichförmig rotierenden Zeigers zustande kommende Bewegungsform.

• A …Länge des Zeigers. (Diese Größe wird auch die Amplitude der harmonischen Schwingung genannt).
• ϕ …(Momentaner) Winkel des Zeigers (im Bogenmaß).
• x …(Momentane) Position des schwingenden Punktes. (Diese Größe wird positiv oder negativ gesetzt, je nachdem, ob der Zeiger nach oben oder nach unten weist. Dabei ist ihr Betrag gleich der Länge des Schattens. Sie wird auch die Elongation der harmonischen Schwingung genannt).
• ω …Winkelgeschwindigkeit der →Rotation des Zeigers. (Diese Größe nennt man auch die Kreisfrequenz der harmonischen Schwingung).

Zeigerdiagramme

Um eine Sinusfunktion im Zeitbereich zu zeichnen, lässt man einen Zeiger mit der Länge 1 rotieren. Da der Sinus definiert ist als Gegenkathete zur Hypotenuse und die Länge des Zeigers die →Hypotenuse darstellt, kann man den Sinus eines Winkels direkt ab der Gegenkathete ablesen.

In Mathematikbüchern findet man in etwa die folgende Definition: Der Steigungswinkel einer Geraden ist derjenige im mathematisch positiven Sinn gemessene Winkel α , den die Gerade mit der positiven x -Achse einschließt.

Die Steigung (der Anstieg) k oder m ist konstant. Wie kannst du bei einer gegebenen Geraden diese Steigung ablesen? Indem du ein Steigungsdreieck einzeichnest. Du wählst dazu einen beliebigen Punkt der Geraden. Sobald du in x-Richtung eine Einheit nach rechts gehst, führt immer die konstante Streckenlänge k in y-Richtung zur Geraden zurück. Du kannst auch mehrere Einheiten in x-Richtung entlang gehen. Die entsprechende Streckenlänge, die in y-Richtung zur Geraden zurückführt, entspricht dann dem k-Fachen der x-Richtung. Dadurch kannst du mit Trigonometrie den Steigungswinkel berechnen.

In der Mathematik, insbesondere in der Analysis, ist die Steigung (auch als Anstieg bezeichnet) ein Maß für die Steilheit einer Geraden oder einer Kurve. Am Betrag der Steigung kannst du erkennen, wie steil der Graph einer lineraen Funktion steigt oder fällt. Je größer der Betrag der Steigung ist, umso steiler steigt oder fällt die Gerade.

Was ist das Problem beim Steigungswinkel?

Das Problem, die Steigung zu ermitteln, stellt sich dabei nicht nur bei geometrischen Fragestellungen, sondern beispielsweise auch in der Physik oder in der Volkswirtschaftslehre. So entspricht etwa die Steigung in einem Zeit-Weg-Diagramm der Geschwindigkeit oder die →Steigung in einem Zeit-Ladungs-Diagramm der Stromstärke.

Steigt die Gerade an (in positiver x-Richtung, also von links nach rechts betrachtet), so ist ihre Steigung positiv. Für eine fallende Gerade ist die Steigung negativ. Steigung 0 bedeutet, dass die Gerade waagrecht, also parallel zur x-Achse verläuft.

Aus der Steigung einer Geraden lässt sich mit Hilfe der Tangens- und Arcustangens-Funktion der zugehörige Steigungs- bzw. Neigungswinkel der Geraden bezogen auf die positive x -Achse berechnen.

Ein Zusammenhang aus der →Trigonometrie besagt, dass in einem rechtwinkligen Dreieck der Tangens von einem der beiden spitzen Winkel gleich dem Quotienten der jeweiligen Gegen- und Ankathete ist, womit klar wird, dass die Steigung zugleich der Tangens des Steigungswinkels (in Grad) gegenüber der positiven x-Achse ist.

In der Mathematik und Geodäsie versteht man unter einem System von polaren Koordinaten (auch: Kreiskoordinatensystem) ein zweidimensionales Koordinatensystem  Punkt in einer Ebene durch den Abstand von einem vorgegebenen festen Punkt und den Winkel zu einer festen Richtung festgelegt wird.

Ein kartesisches Koordinatensystem ist ein orthogonales Koordinatensystem. Im zwei- und dreidimensionalen Raum handelt es sich um das am häufigsten verwendete Koordinatensystem, da sich viele geometrische Sachverhalte in diesem anschaulich und übersichtlich beschreiben lassen.

Der feste Punkt wird als Pol bezeichnet; er entspricht dem Ursprung bei einem kartesischen Koordinatensystem. Der vom Pol in der festgelegten Richtung ausgehende Strahl heißt Polarachse. Der Abstand vom Pol wird meist mit r bezeichnet und heißt Radius oder Radialkoordinate, der Winkel wird mit φ bezeichnet und heißt Winkelkoordinate, Polarwinkel, Azimut oder Argument.

Umrechnung von kartesischen in polare Koordinaten

Die Umrechnung von kartesischen Koordinaten in Polarkoordinaten ist etwas schwieriger, weil man mathematisch gesehen dabei immer auf eine (nicht den gesamten Wertebereich des Vollwinkels umfassende) trigonometrische Umkehrfunktion angewiesen ist. Zunächst kannst du aber der Radius r mit dem Satz des Pythagoras einfach berechnen.

Die Polarkoordinaten (Kreiskoordinaten) eines Punktes in der euklidischen Ebene werden in Bezug auf einen Koordinatenursprung (einen Punkt der Ebene) und eine Richtung (einen im Koordinatenursprung beginnenden Strahl) angegeben.

Polarkoordinaten bilden einen Spezialfall von orthogonalen krummlinigen Koordinaten. Sie sind hilfreich, wenn sich das Verhältnis zwischen zwei Punkten leichter durch Winkel und Abstände beschreiben lässt, als dies mit

x- und y-Koordinaten der Fall wäre. In der Geodäsie sind Polarkoordinaten die häufigste Methode zur Einmessung von Punkten (Polarmethode). Wobei in der Funknavigation wird das Prinzip oft als „Rho-Theta“ (für Distanz- und Richtungsmessung) bezeichnet.

In der Mathematik misst man die Winkelkoordinate im mathematisch positiven Drehsinn (Gegenuhrzeigersinn). Benutzt man gleichzeitig ein kartesisches Koordinatensystem, so dient in der Regel dessen Koordinatenursprung als Pol und die x-Achse als Polarachse. Die Winkelkoordinate misst man also von der x-Achse aus in Richtung der y-Achse. In der Geodäsie und in der Navigation wird das Azimut von der Nordrichtung aus im Uhrzeigersinn gemessen.

Unter einem Bruchterm versteht man einen Bruch aus Zähler und Nenner bei dem im Nenner mindestens eine Variable vorkommt. Einen Bruchterm zu kürzen, bedeutet, den Zähler und Nenner des Bruchs durch einen gemeinsamen Teiler zu dividieren. 

Unter Bruchtermen versteht man eigentlich nur solche Terme mit Brüchen, bei denen die Variable auch im Nenner vorkommt. Bruchterme, also Rechenausdrücke in der Form von gemeinen Brüchen, spielen in der elementaren Algebra eine wichtige Rolle. Im Allgemeinen enthalten Bruchterme neben Zahlen auch Variablen. Die Rechenregeln für →Brüche können auch auf Bruchterme angewendet werden.

Zwei Brüche werden miteinander multipliziert, indem man sowohl die beiden Zähler, als auch die beiden Nenner miteinander multipliziert.  Brüche solltest du vor dem Multiplizieren Kürzen.

Wie berechne ich einen Bruchterm?

Wenn man Zähler und Nenner mit der gleichen Zahl/Variable multipliziert, verändert sich der Wert des Bruchterms nicht. Die Erweiterung von Bruchtermen ist erforderlich, wenn Bruchterme mit ungleichnamigen Nenner auf einen gemeinsamen Nenner gebracht werden sollen.

Zwei Brüche mit gleichem Nenner werden addiert, indem man ihre Zähler addiert. Der Nenner verändert sich bei der Addition nicht. Er wird einfach beibehalten.

→Kürzen von Bruchtermen: Bruchterme werden gekürzt, indem man Zähler und Nenner durch demselben Faktor (Zahl, Variable, Term) dividiert.

Wie dividiert man Bruchterme? Dies macht man, indem man mit dem Kehrwert multipliziert. Dabei werden vom zweiten Bruch Zähler und Nenner vertauscht. Im Anschluss multiplizieren wir Zäher mit Zähler und wir multiplizieren Nenner mit Nenner. Da Zähler und Nenner gleich sind kann man auf 1 kürzen.

Wann ist ein Bruch nicht definiert? Da Bruchterme oftmals eine oder mehrere Variablen im Nenner vorweisen, ist deren →Definitionsmenge häufig auch eingeschränkt. Bereits in der Grundschule hat man ja in Mathe gelernt, dass der Nenner eines Bruchs nicht gleich null werden darf. Ist nämlich dies der Fall, dann ist dieser Bruch nicht definiert.

Wie Addiert man Brüche mit variablen? Indem du ihre Zähler addierst. Der Nenner verändert sich bei der Addition nicht. Er wird einfach beibehalten. Nach dem Addieren lässt sich der Bruch oftmals noch vereinfachen.